承诺

承诺分为三个步骤：承诺，打开承诺，验证承诺。

承诺：承诺:发送方将某个值 $x$ 封装为 $y$ 发送给接收方。(1)发送方不能修改信封中的值(绑定性);(2)接收方无法知道 $x$ (隐藏性)。

打开承诺:发送方揭露 $x$ 。

校验承诺:接收方校验打开的值 $x$ 与 $y$ 中封装的 $x$ 是否相同。

承诺一个值

对函数有一定要求：

承诺一个多项式

承诺：选择 $n+1$ 个随机数 $a_0,a_1,...,a_n$ ，构造多项式 $f(x)=\Sigma_{i=0}^na_ix^i$ ，计算 $A_i=a_iG,\ i=0,...,n$ ，发送 $A_i$
打开承诺：打开一个随机点 $k$ ，计算 $f(k)=\Sigma_{i=0}^na_ik^i$ ，发送 $(k,f(k))$
校验承诺：基于 $A_i$ ，校验 $(k,f(k))$ 正确性， $f(k)G=\Sigma_{i=0}^n(k^iA_i)$

如果攻击者不知道多项式,选择随机数作为函数值,则发生碰撞的概率可忽略。

因此,不必打开多项式所有系数,仅打开一个或多个函数点即可,从而减少发送数据。

此外,没泄露多项式,具有保密性。需要 n+1 个值,才会泄露多项式的系数。

哈希承诺

哈希函数求逆满足NP困难

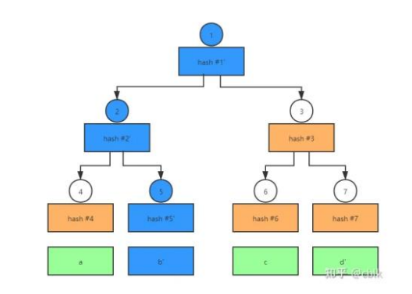
问题：证明方证明知道每个叶子的值 $x_i,i0=,..,2^n$

低效做法：

高效做法：

发送数据和校验复杂度均降低。

如果每个叶子的取值是 0 或 1,则 n 次均成功概率为 $1/2^n$ 。

如果每个叶子的取值空间为m,则 n 次均成功概率为 $1/m^{20}$ 。

核心思想：从概率角度，不必打开全部叶子节点；仅需要打开 n 个点，如果每次都正确，则伪造成功概率指数降低。因此，验证方相信证明方知道所有叶子节点。

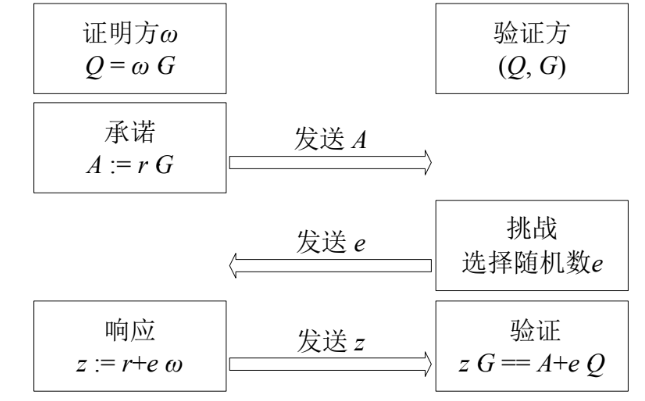
承诺 $A=rG$ ，挑战 $e$ ，相应 $z=r+e\omega$ ，校验 $zG=A+eQ$

初始化：椭圆曲线生成元为 $G,H,H=\alpha G$ ，其中 $\alpha$ 保密

Pedersen承诺的同态性

初始状态：A和B的余额密文是0

C对 $m_1$ 个Token承诺： $P_1=m_1G+r_1H$ ，接收地址为 $Addr_{Alice}$ ，然后签名广播。打开承诺：私底下保密发送 $m_1,r_1$ 给A，A校验Pedersen承诺的一致性，且等交易单上链后，则收款成功
D对 $m_2$ 个Token承诺： $P_2=m_2G+r_2H$ ，接收地址为 $Addr_{Alice}$ ，然后签名广播。打开承诺：私底下保密发送 $m_2,r_2$ 给A，A校验Pedersen承诺的一致性，且等交易单上链后，则收款成功

经过共识算法：矿工上链A余额密文： $P_1+P_2=(m_1+m_2)G+(r_1+r_2)H$

A知道秘密， $m_1+m_2$ 和随机数 $r_1+r_2$ ，则A能花费该费用。

A对 $m_3$ 个Token承诺： $P_3=m_3G+r_3H$ ，接收地址为 $Addr_{Bob}$ ，然后签名广播，打开承诺：私底下保密发送 $m_3,r_3$ 给B，B校验Pedersen承诺的一致性，且等交易单上链后，则收款成功

经过共识算法：矿工上链A和B余额密文：

A:P_1+P_2-P_3=(m_1+m_2-m_3)G+(r_1+r_2-r_3)H\\ B:P_3=m_3G+r_3H

如果 $\alpha$ 泄露：

A知道 $G,H$ 之间的离散对数 $\alpha$ ，后果很严重。

真实情况，A拥有小金额 $m=10$ 和随机数 $r$ ，余额承诺为 $P=mG+rH$

A能够计算 $\alpha^{_1}$ ，选择一个大金额 $m^{\prime}=200000$ ，计算随机数 $r^{\prime}=r-(m^{\prime}-m)\alpha^{-1}$

A支付 $m^{\prime}$ 个Token，支付承诺为 $P=m^{\prime}G+r^{\prime}H$ ，接收地址为 $Addr_{Bob}$ ，然后签名广播，打开承诺：私底下保密发送 $m^{\prime},r^{\prime}$ 给B，B校验Pedersen承诺的一致性，且等交易单上链后，则收款成功

经过共识算法：矿工上链B余额密文： $P=m^{\prime}G+r^{\prime}H$

m^{\prime}G+r^{\prime}H=m^{\prime}G+(r-(m^{\prime-m})\alpha^{-1})H\\ =m^{\prime}G+rH-m^{\prime}\alpha^{-1}H+m\alpha^{-1}H\\ =mG+rH=P

类似结论：zcash中各个生成元 $g_i,h_i$ 之间的离散对数不能泄露