同态加密GSW方案

本文将介绍同态加密中的一个方案——GSW，它利用近似特征向量技术，设计了无需计算密钥的全同态加密方案。原论文：《Homomorphic Encryption from Learning with Errors: Conceptually-Simpler, Asymptotically-Faster, Attribute-Based》

GSW整体思想

基本思想

矩阵有着这样的一个性质：一个矩阵CC乘以vv等于一个特征值乘以vv，vv是这个矩阵的特征向量，μ\mu是特征值:C⋅v=μ⋅mod qC\cdot v =\mu \cdot mod \ q

那么，我们现在可以把CC看作密文，vv看作密钥，要加密的消息是μ\mu:

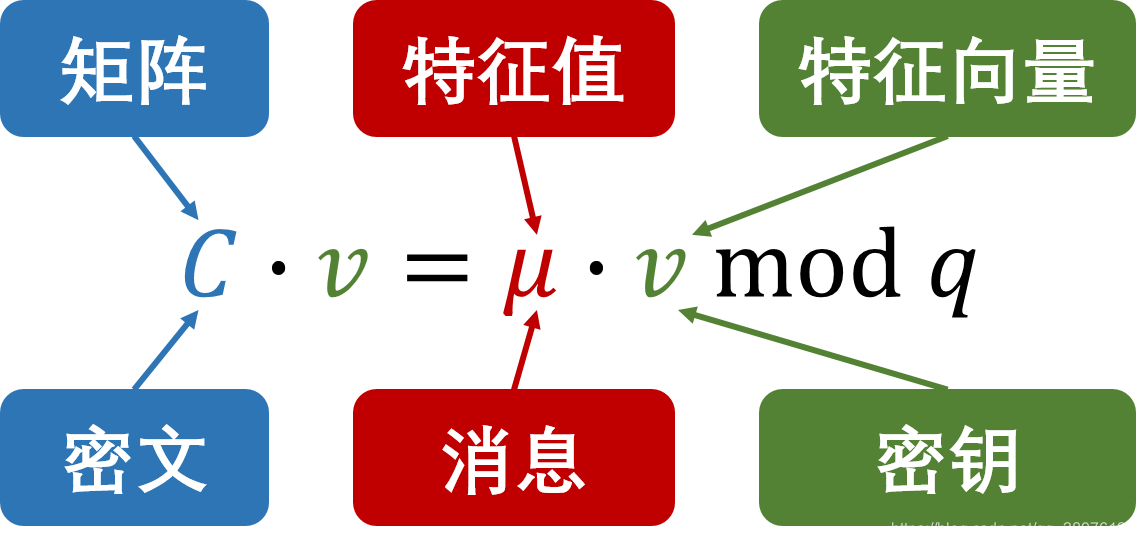
很容易可以发现这个形式具有同态的性质：密文的加或乘相当于明文的加或者乘。

C1⋅v=μ1⋅v mod qC2⋅v=μ2⋅v mod qC1⋅C1⋅v=μ1⋅μ2⋅v mod qC_1\cdot v=\mu_1 \cdot v\ mod \ q \\ C_2\cdot v=\mu_2 \cdot v\ mod \ q \\ C_1\cdot C_1\cdot v=\mu_1\cdot \mu_2 \cdot v\ mod \ q

然而，这个形式虽然具有同态的性质，但是很明显非常的不安全，因为找到一个矩阵的特征向量很简单，密钥很容易得到。为了保证安全性，我们可以将其转换为 LWE 的形式：

C⋅v=μ⋅v+e mod qC\cdot v =\mu \cdot v +e \ mod \ q，

其中，CC代表密文，μ\mu代表消息，ee代表密钥，是系数很小的噪声向量(e<<qe<<q)，vv是一个近似特征向量。

同态性质

我们来验证一下这个方案的同态性质：

C1⋅v=μ1⋅v+e1 mod q, C2⋅v=μ2⋅v+e2 mod qC_1\cdot v =\mu_1 \cdot v +e_1 \ mod \ q,\ C_2\cdot v =\mu_2 \cdot v +e_2 \ mod \ q

加法运算:(C1+C2)⋅v=(μ1+μ2)⋅v+(e1+e2) mod q(C_1+C_2)\cdot v=(\mu_1+\mu_2)\cdot v +(e_1+e_2)\ mod\ q

乘法运算：(C1×C2)⋅v=C1⋅(μ2⋅v+e2)=(μ1⋅μ2)⋅v+(μ2⋅e1+C1⋅e2)(C_1 \times C_2)\cdot v =C_1\cdot (\mu_2\cdot v+e_2)=(\mu_1\cdot \mu_2)\cdot v+(\mu_2\cdot e_1+C_1\cdot e_2)

同态加法和乘法满足，但乘法会导致额外噪声的出现。

噪声处理

为了让这个噪声项尽量小，我们对这个新的噪声进行分析：

  • 可以减小μ2\mu_2，即让消息空间变小。要达到这个目的仅需将消息空间设置成{0,1}\{0,1\}即可。GSW 方案中使用与非门 (NAND gats) 可将消息空间设置成{0,1}\{0,1\}。
  • 可以使密文 CC变小。密文可能是两个密文的乘法，即使初始的密文很小，计算后也可能得到较大的密文。是否能有什么技术能够使得密文一直保持在很小的范围内（甚至在 {0, 1} 内）？文中提出一种 Flatten ciphertext 的技术。

密文大小限制

限制密文大小：分解技术

我们有以下定义：

a∈Zqka\in Z^k_q其中k是维度，q是模。l=logq+1l=log_q+1是q的对数，N=k⋅lN=k\cdot l

有一些函数：

  • BitDecomp(a)=(a1,0,...,a1,l−1,...,ak,0,...,ak,l−1)BitDecomp(a)=(a_{1,0},...,a_{1,l-1},...,a_{k,0},...,a_{k,l-1})是a的每个系数的比特分解，从低位到高位
  • BitDecomp−1(b∈ZqN)BitDecomp^{-1}(b\in Z^N_q)是上面分解函数的逆分解
  • Flattern(b∈ZqN)=BitDecomp(BitDecomp−1(b))Flattern(b\in Z^N_q)=BitDecomp(BitDecomp^{-1}(b))是一个系数都在{0,1}\{0,1\}中的向量
  • Powersof2(s)=(s1,2s1,...,2l−1s1,...,sk,2sk,...,2l−1sk)Powersof2(s)=(s_1,2s_1,...,2^{l-1}s_1,...,s_k,2s_k,...,2^{l-1}s_k)

然后我们给出近似特征向量的一个特殊形式：v=Powersof2(s)v=Powersof2(s)其中s是随机的

开始 Flatten Ciphertext （展平密文）：

  • 假设对于一个与非门（NAND）： $C^{NAND}=I_N-C_1\cdot C_2\ mod\ q $
  • 令 C3←Flatten(CNAND)C_3\larr Flatten(C^{NAND})为CNANDC^{NAND}每一行的展开结果，C3C_3中所有的系数都在集合{0,1}\{0,1\}中
  • C3⋅v=CNAND⋅v mod qC_3\cdot v=C^{NAND}\cdot v\ mod\ q我们没有改变加密的消息，甚至没有增加噪声。

GSW加密方案

  • Setup(1n,1L)Setup(1^n,1^L)，选择k=k(λ,L)k=k(\lambda,L)bit的模q，格的维度参数是n=n(λ,L)n=n(\lambda,L)，适当的为LWE取误差分布X=X(λ,L)X=X(\lambda,L)使得在已知攻击下达到2λ2^{\lambda}的安全性。同时，选择参数m=m(λ,L)=O(nlogq)m=m(\lambda,L)=O(nlogq)，参数params=(n,q,X,m)params=(n,q,X,m)，令l=logq+1,N=(n+1)⋅ll=log_q+1,N=(n+1)\cdot l

  • KeyGen(params)KeyGen(params)，采样t←Zqnt\larr Z^n_q，输出sk=s←(1,−t1,...,−tn)∈Zqn+1sk=s\larr (1,-t_1,...,-t_n)\in Z_q^{n+1}，v←Powersof2(s)∈ZqNv\larr Powersof2(s)\in Z_q^N

  • PubKeyGen(params,sk)PubKeyGen(params,sk)，均匀生成一个矩阵B←Zqm×nB\larr Z^{m\times n}_q和一个向量e←χme\larr \chi ^m，设b=B⋅t+eb=B\cdot t+e，设A为（n+1）列矩阵，设置公钥pk=Apk=A，公钥可以看作一个LWE实例，是由向量组成的矩阵，且与密钥点积得到的结果很小。

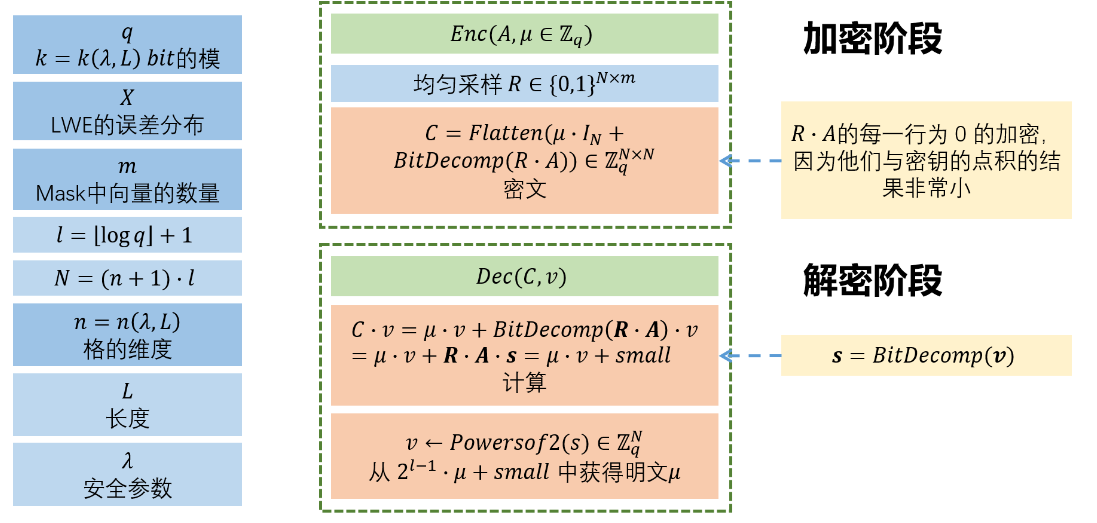
  • Enc(A,μ)Enc(A,\mu)，为了加密消息μ∈Zq\mu\in Z_q，均匀采样一个矩阵R∈{0,1}N×mR\in \{0,1\}^{N\times m}，可得A⋅RA\cdot R的每一行为0的加密，因为他们与密钥的点积的结果非常小，同时输出如下密文:

C=Flatten(μ⋅IN+BitDecomp(R⋅A))∈ZqN×NC=Flatten(\mu \cdot I_N+BitDecomp(R\cdot A))\in Z_q^{N\times N}

  • 解密Dec(C,v)Dec(C,v)，计算C⋅v=μ⋅v+BitDecomp(R⋅A)⋅v=μ⋅v+R⋅A⋅s=μ⋅v+smallC\cdot v=\mu \cdot v+BitDecomp(R\cdot A) \cdot v =\mu \cdot v+ R\cdot A\cdot s=\mu \cdot v+small

image-20230725195628371

  • 同态操作：在密文上进行加法/乘法后，展平密文。

加法，Add(C1,C2)=Flattem(C1+C2)Add(C_1,C_2)=Flattem(C_1+C_2)，噪音为e1+e2e_1+e_2，增长因子为20